今回は、重回帰分析の結果について詳しくみていきたいと思います。
Excelの「データ分析」による重回帰分析の結果は、次のように出力されます。

重回帰式は次の一次式で表されます。
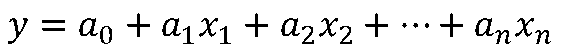
上記の分析結果からは、具体的には以下のような式になります。
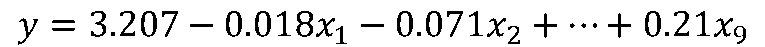

回帰統計
重相関Rは、-1~1の間の値をとり、プラス・マイナスのそれぞれ1に近いほど相関が強いことを示しています。
一般に絶対値が0.7以上あれば相関が強いと言われています。
なお、説明変数同士で強い相関(0.9以上)がある場合、分析が正しく行われないため(多重共線性:Multi-Collinearityマルチコと呼ばれる。Collisionは衝突の意。Collinearity はLinearityとの合成語)、どちらか一方の変数を除外します。
重決定R2は、重相関Rを二乗した値です。
二乗することで常に正の値として相関の強さを表し、決定係数あるいは寄与率と呼ばれます。
0.7の二乗が0.49であることから、重決定R2は0.5以上あれば相関が強いとされます。
決定係数(重決定R2)は、回帰分析から得られた回帰式が目的変数の変動をどの程度説明できているかを表す指標です。
補正R2は、自由度調整済み決定係数と呼ばれ、
決定係数(重決定R2)を自由度(標本数 -1- 説明変数の数)で調整した決定係数です。
通常は、決定係数(重決定R2)で回帰式の精度をみますが、複数の説明変数を扱う重回帰分析では、説明変数が増えると決定係数が1に近づくという性質があるため自由度を基に調整します。
重回帰分析ではこの補正R2をみて判断するようにします。
この例では補正R2は0.018225なので、この重回帰分析で得られた式は、1.8%程度の説明能力しかありません。\(y\)を予測する式としてはほとんど意味をなさない式と言えます。
なお、Excelの重回帰分析では説明変数を16個まで指定できます。それ以上の説明変数がある場合は、分割して実行する必要があります。
分散分析表
分散分析表は、一元配置分散分析の際にも出てきました。
重回帰分析でも複数のデータ群(説明変数:資料9分野)に対して分散分析と同様の処理を行っています。
ここでの有意Fは帰無仮説「全ての説明変数の平均に差はない」即ち「回帰分析に使用した説明変数の組み合わせに意味はない」という確率を表すもので、F分布におけるP値のことです。
有意水準0.05以内であれば帰無仮説を棄却できるのですが、有意F=0.138ですので帰無仮説を棄却できず受容することになります。
即ちここでも、回帰分析に使用した説明変数の組み合わせに意味はない、という結果です。
残差と変動
下図のように、実際のデータと予測値との差を残差と言います。
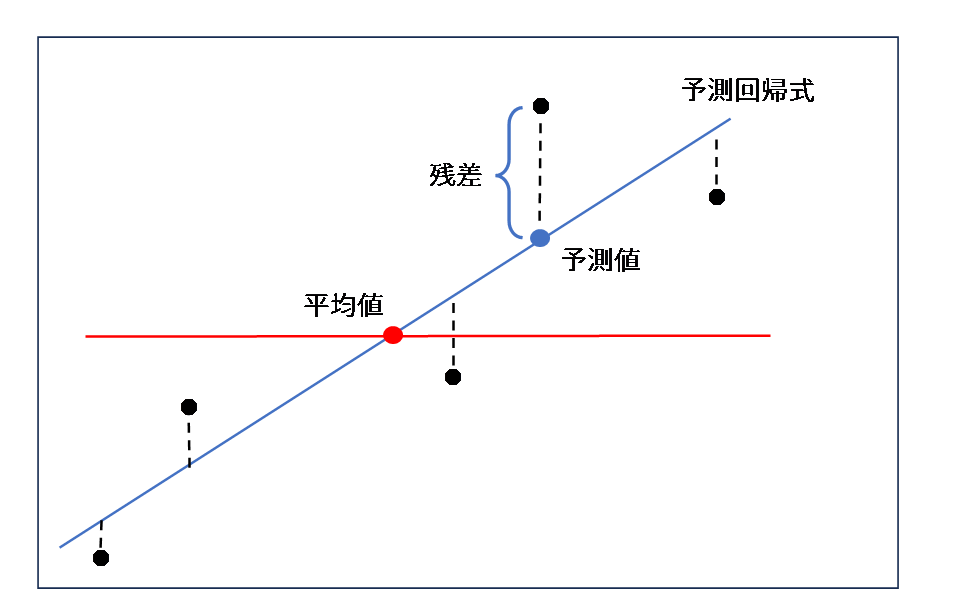
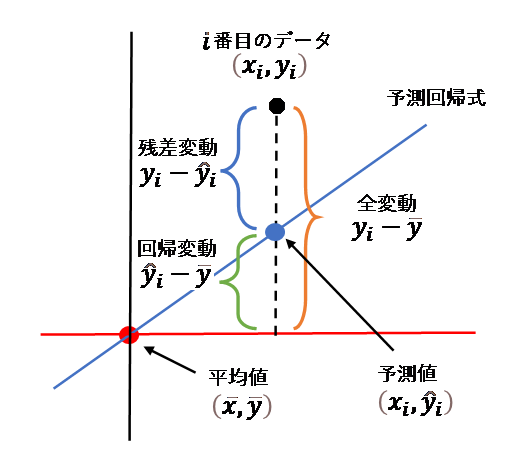
分散分析表にある変動には以下の関係式が成り立ちます。
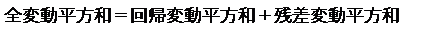
出力結果では、全変動 = 14.72174 + 264.41444 = 279.1362 となっています。
式で書くと次のようになります。
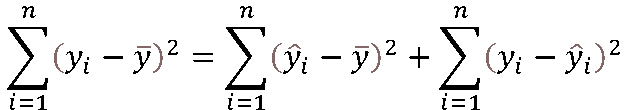
決定係数(重決定R2)は、説明変数が目的変数をどれくらい説明しているかを示すものです。
それは図を見て分かるように残差変動が少ないほど、即ち全変動に対する回帰変動が多いほど当てはまりが良いことを表しています。
従って決定係数(重決定R2)は、次のように回帰変動を全変動で割ることで求められます。
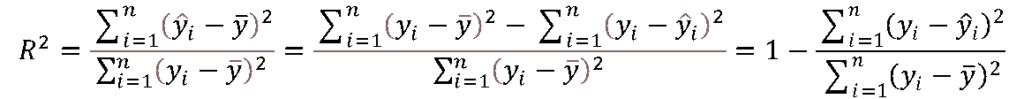
即ち、以下の式になります。
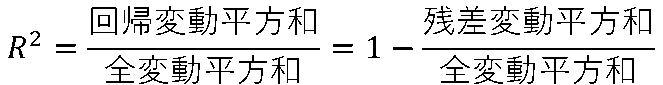
出力結果では、
決定係数(重決定R2)\(R^2\) = 1 ー 264.4144 / 279.1362 = 0.05274 になっています。
自由度調整済み決定係数
自由度調整済み決定係数(補正R2)は次の式から求められます。\(n\)はデータの個数、\(k\)は説明変数の数を表します。
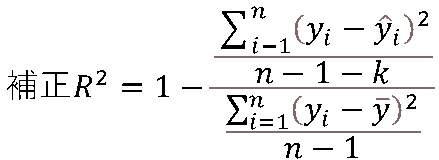
出力結果から、自由度調整済み決定係数(補正R2)は以下のように計算されます。
1 ー (264.4144 / (257-1-9)) / (279.1362 / (257-1)) = 0.018225
t検定
3つ目の表はt検定の結果です。
t値は一般に以下の式で求めることができます。

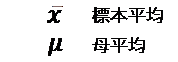
重回帰分析では係数の平均に対して次のようになります。

従って、係数は次式で求めることができます。
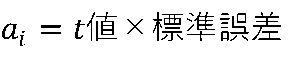
例えば、
小説の係数 = t値 × 標準誤差 = -0.13232 × 0.133464 = -0.01766
となります。
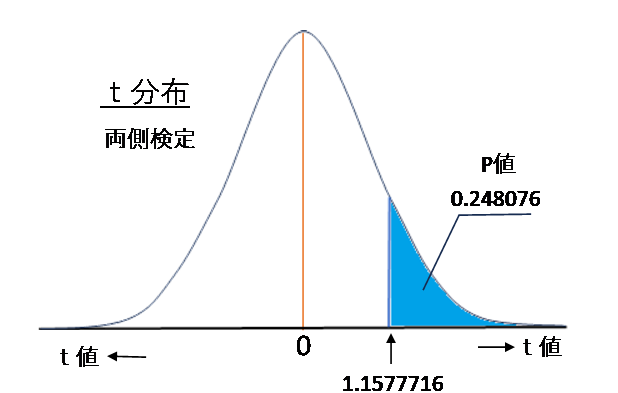
P値
ここでの帰無仮説は「係数が0に等しい」です。即ち、「回帰分析に使用した説明変数に意味はない」です。
それではt検定によって出力された各説明変数のP値を確認してみましょう。これまでと同様にP値は帰無仮説の生起確率です。
P値の全体を見渡すと、有意水準5%を満たす説明変数は語学のみとなっています。これでは \(y\)の式に意味がないのも当然です。\(y\)の式を意味のあるものにするためには、有意な説明変数を揃える必要があるのです。
Excelでt値からP値を求めるには両側検定の次の関数を使います。
P値 = T.DIST.2T(絶対値のt値、調整自由度)
調整自由度 = データ数-1-説明変数の数
児童書の場合、P値 = T.DIST.2T (1.1577716,257-1-9) = 0.248076 となります。
逆にP値が0.05になる時のt値は次の関数で求めることができます。
t値 = T.INV.2T (0.05,257-16-1) = 1.969897
t値の場合は、値が2.0以上あれば有意と判断することができるということです。
95%信頼区間
さて、これまでの出力結果をみると有意な結果は「語学」だけであり、全体的には意味のない回帰式であるという事になります。
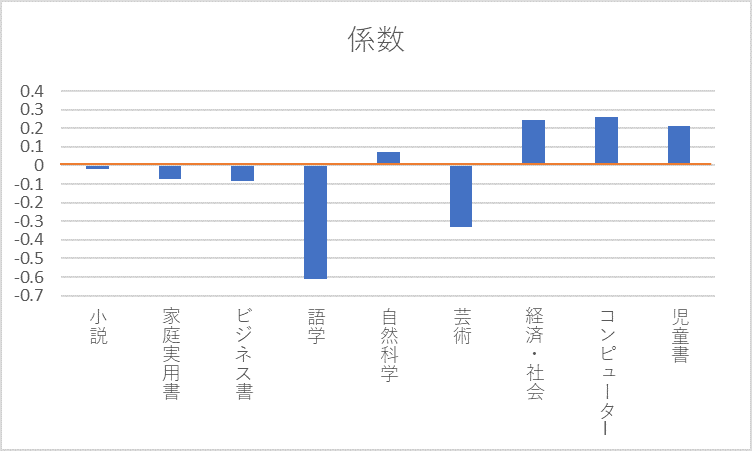
しかし前回は、有意でなくても係数やt値をグラフ化して原因解明のツールとして利用できると推奨しました。
係数がプラスであれば満足度を上げる要因であり、マイナスであれば満足度を下げる要因であると判断して良いだろうと。
それは、図書館において例えば「100人中95人が同意しないと正しいとは言えない」といういうような判定は必要か、という疑問に端を発しています。
図書館利用者の多様な利用行動のなかでは、5%という有意な結果を見出すことはそう多くはないのです。
それでも分析結果から利用者の傾向を読み取ることができるのであれば、それ自体が有益な情報であり、必ずしも厳密に判定すべきものとする必要はないと考えるからです。
下図のように重回帰分析結果の係数をグラフ化し、「満足度に大きな影響を与える要因はどれか」が分かるということが重要なのです。
それでもこのP値の信頼性がどの程度なのかを知っておく必要はあるでしょう。それを信頼区間95%のデータで確認してみましょう。
信頼区間95%とは、100回アンケートを取ったとして、95回はこの範囲におさまっている、というものです。
係数に対する下限および上限95%の数値をグラフ化してみます。グラフ化にあたってはExcelの株価のグラフ作成用を援用しました。

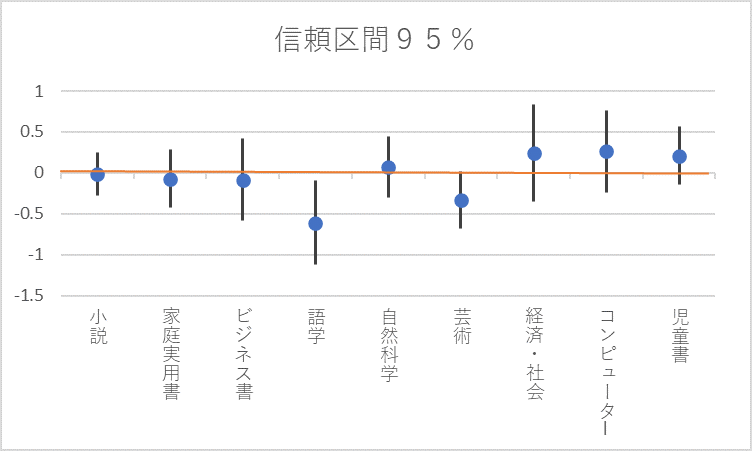
語学と芸術以外は0を跨いでいますので、厳密には満足度を上げているか下げているかは明確に断じることはできない状態です。
それでもこの意味をなさないとされる回帰式が私たちにとって有用なのは、私たちが〇か×かの厳密な判断を目的としているのではなく、利用者の傾向を読み取ることができるということに意味があると考えるからです。
かつて著作権の関係で語学学習書に付属するCD は取り外して貸し出していた時期がありました。CDが無くてがっかりした利用者は多かったでしょう。
「芸術」も美術、音楽、写真、工芸など幅が広いので、不満の明確な理由を追及したい場合は、アンケートではもう少し細かく分野を分けて質問する必要があります。
次回は、図書館におけるアンケートと分析にまつわる話をしたいと思います。