重回帰分析は、予測や原因の究明などに利用される手法です。図書館においても満足度に影響を与える要因の解明などに広く活用できる手法です。
分析の結果は統計学を知らなくても容易に理解できるものですので、図書館現場では心強い分析ツールになります。
次のようなアンケート・データを用いて重回帰分析をみていきます。
(1)所蔵資料の満足度を5段階評価(5:満足、4:まあ満足、3:普通、2:やや不満、1:不満、0:未回答)
(2)今後力を入れて欲しい分野を選択(複数選択可、制限無し)
選択項目は名義尺度なので、ダミー変数として選択した分野に1を設定します。
例えば、ID=7の人は小説と児童書に力を入れて欲しいと選択していたので、小説と児童書の欄に1を設定しています。また、資料全般に対する満足度の評価は4でした。

重回帰分析の手順
Excelの「データ分析」で回帰分析を選択します。
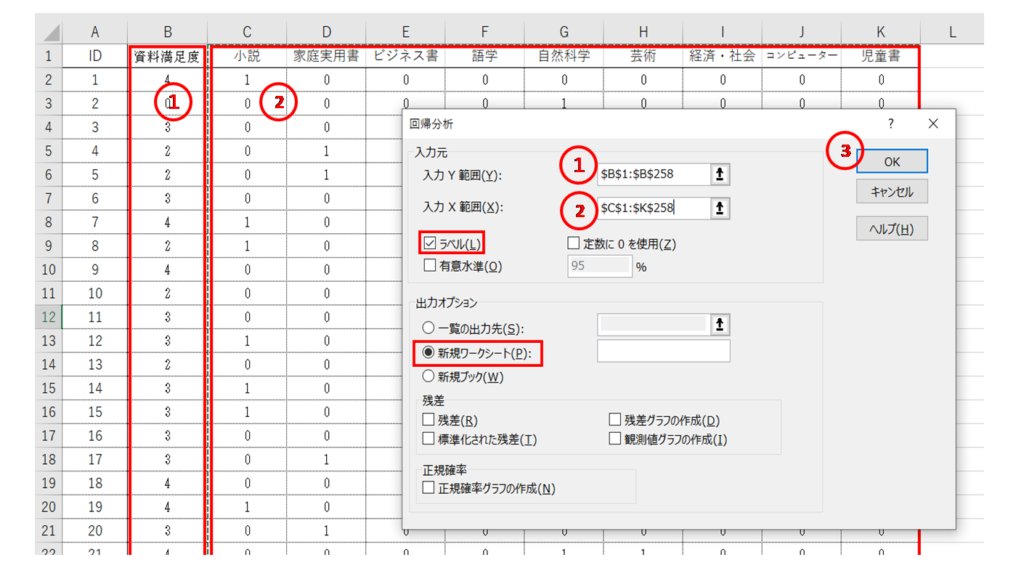
設定は以下のように行います。
「入力Y」の変数を目的変数と言います。「入力X」の複数の変数を説明変数と言います。
結果は以下のとおりです。

重回帰式は次の一次式で表わされます。
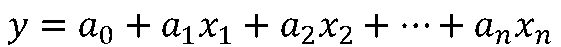
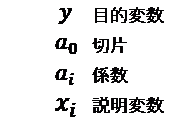
今、\(y\)を満足度、\(x_i\)を資料の各分野とすると、係数がプラスの分野は満足度を上げる要因であり、マイナスの分野は満足度を下げる要因になることが分かります。
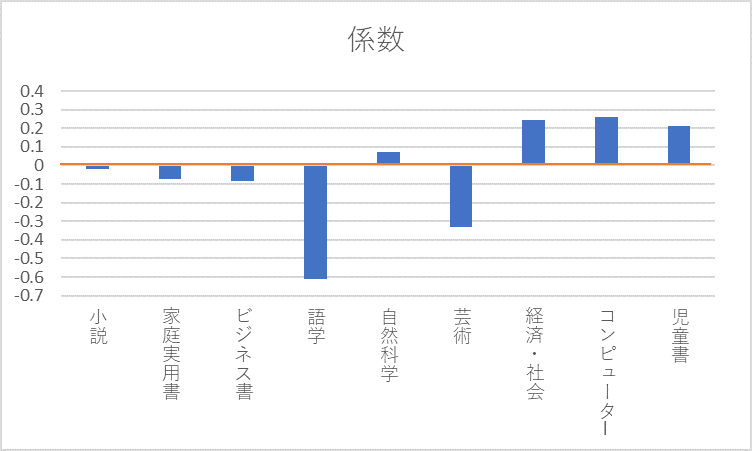
そこで係数の値をグラフにすると以下のようになります。
グラフにすると語学と芸術が満足度を下げる主な要因であることが一目で分かります。
経済・社会、コンピューター、児童書は満足度を上げる要因になっています。
係数は、効果の大きさを表わしており、例えば説明変数である児童書の例では、変数(ここでは児童書を選択する人)が1増えるごとに平均0.21037ずつ目的変数の値が増えることを意味しています。
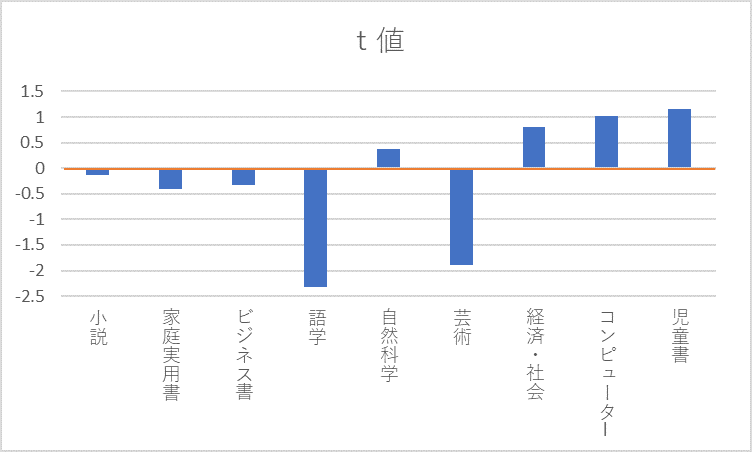
満足度へは分野を選択する人数が関係してきます。その影響は、\(a_ix_i\)の積で効いてきます。この時、影響の大きさをt値で判断します。
同様にt値をグラフにすると以下のようになります。
係数とt値のグラフを見比べると同じような形状をしています。この二つのグラフを、目盛を合わせて重ねると次のようになります。
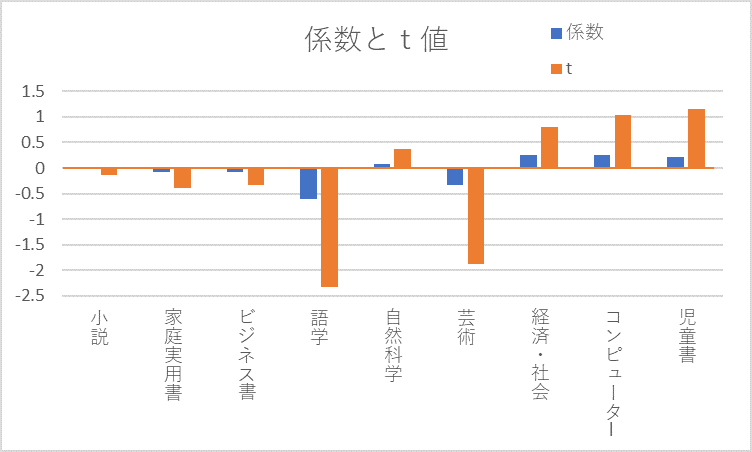
数値としてはt値の方が大きくなりますが、判断材料としてはどちらを採用しても問題はなさそうです。
ただ、特に個別要因の効果の大きさを見たい時は係数を、選択した人数を加味した影響の大きさを知りたい場合はt値を見るということはあるでしょう。
影響は係数と変数の積なので、効果は大きいが影響は小さい、あるいはその逆などが考えられます。
重回帰分析の効用
重回帰分析を行って係数やt値を得ることで、優先度の決定や焦点の絞り込みが容易になり、原因の究明もしやすくなります。
グラフの判断には統計学の知識は特に必要がなく、また重回帰分析はExcelで実行できるため誰でも身近に使うことができて、選書の際の判断などに利用することで満足度向上の取り組みに役立たせることができます。
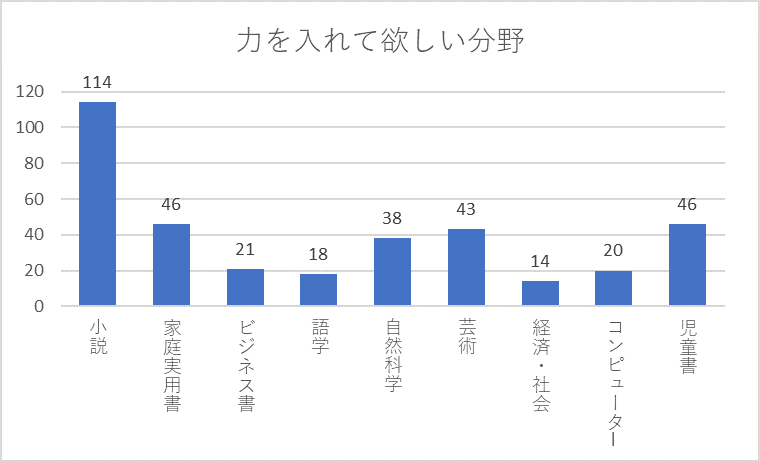
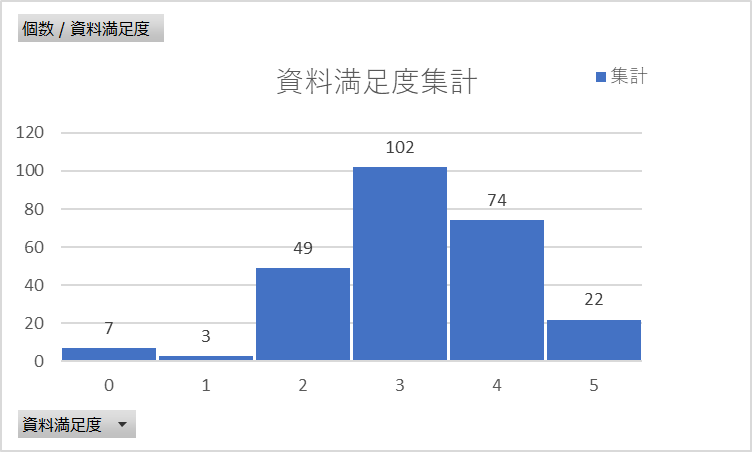
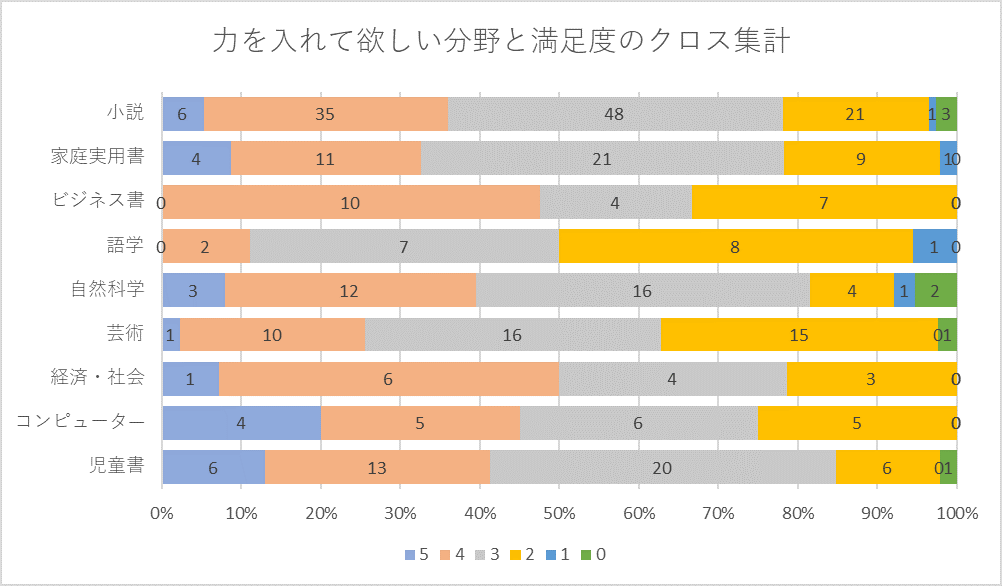
下図は、力を入れて欲しい分野および資料満足度の度数分布です。また、この両者のクロス集計表を示しています。
語学の分野は「5.満足」が0人で「2.やや不満」「1.不満」がもっとも多いので、問題がありそうだということは分かります。
このようにクロス集計は原因を探すきっかけとして役立つのですが、しかし、常に分かりやすいかというとそうとは限りません。これらの情報からの問題発見には困難な場合も多く、判断がしづらいことが多いのです。
重回帰分析では、他にも接遇と力を入れて欲しいサービスとの関係を調べるなどさまざまな要因に対して分析を行うことができるので、図書館での分析の主要な武器として普段から使いこなせるようにしておきたいところです。
次回は、重回帰分析についてもう少し説明をしたいと思います。