t検定
t検定は、正規分布とされる2つの標本の平均値の差を検定します。
対応のあるt検定で対になる標本とは、同一グループを対象とした調査で午前と午後で時間的な影響があるかどうかを調べるような対になっている標本のことです。
ここでは、対応のないt検定をみていきます。
なお、5段階評価のような順序尺度のデータは、数量データとして扱うのは理論上適切ではないので、特定の分布に拠らないノンパラメトリックなマンホイットニー検定などを用いるのが妥当とされます。
しかし、一般には順序尺度のデータを数量データとみなして処理することも広く行われています。ここでのt検定は、満足度を数量データとして処理したものです。
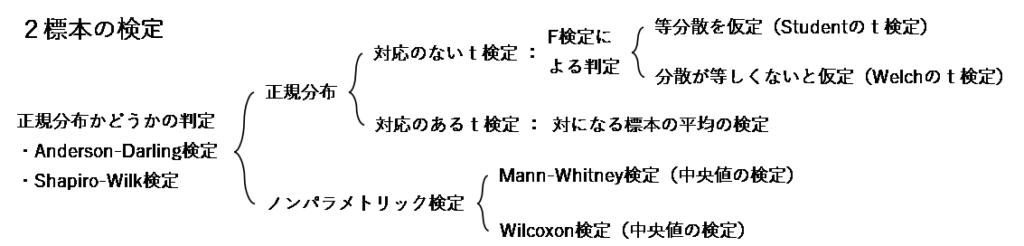
F検定による分散判定
対応のないt検定の場合、分散が等しいと仮定するかどうかで処理が分かれます。その分散の判定にF検定を用います。
Excelのデータ分析を使ってF検定を行います。
有意水準を0.05とし、「ラベル」にチェックを入れます。
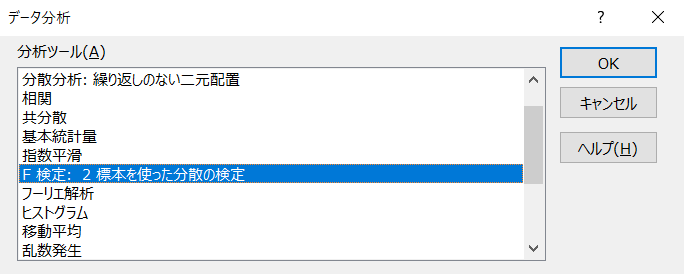
結果は以下のとおりです。
帰無仮説は、「2標本の分散は等しい」です。判定はP値で行います。P値は帰無仮説が成り立つ確率でした。
R3-R4およびR3-R5の2標本間では、P値がそれぞれ0.010534、9.73x\(10^{-5}\)で0.05以下となり帰無仮説は棄却されますので、この2つの標本間には有意な差がある(分散は等しくない)と判断されます。
一方、R4-R5の2標本間では、P値が0.1025で0.05を超えていますので分散が等しいことが棄却できず、等分散が仮定されます。



次に、F検定による等分散の判定に従って2種類のt検定を行います。
t検定では2標本の平均値の差の検定を行います。
設定は、いずれも有意水準を0.05とし、「二標本の平均値の差」を0に設定します。
0は「二標本の平均値は等しい」という帰無仮説の設定です。設定を行わなかった場合は、デフォルトとして0が設定されます。
「ラベル」にチェックを入れるのを忘れないようにしましょう。
【分散が等しくないと仮定した場合の設定】


【等分散が仮定される場合の設定】


結果は以下の通りです。
等分散を仮定した場合は、2標本の分散は等しいという仮定ですので、共通の分散値として2つの中間の値が「プールされた分散」に示されます。
等分散を仮定した場合と仮定しない場合とでのt検定の結果の比較も行ってみました。
両者に目立った大きな違いはないのでF検定を行うまでもなく、分散は等しくないという仮定で行うt検定で十分とする判断もあるようです。
t検定:分散が等しくないと仮定した
2標本による検定
t検定:等分散を仮定した2標本に
よる検定






検定の結果
t検定の判定はP値で行い、両側検定の結果をみます。
判定は、片側検定よりも両側検定の方がより厳しい判定になりますが、どちらで判定するかは予め決めておきます。対立仮説側からは、「差がある」「より大きい」「より小さい」という3つの判断があり、大小を検証する場合は片側検定を用いるのでした。
結果からは、R3-R4、R4-R5の1年ごとの判定では明確な差があるとは示されませんでしたが、R3-R5の3年間でみると明らかに資料の満足度が上昇していることが検証できました。
R3-R4の片側検定では有意な差が認められますので、全体的に上昇傾向にあると言って良いでしょう。ただし、R5年で上昇率が落ち着いてきた兆しが見えるので、今後の取り組みを改めて確認してみるのが良いでしょう。
95%信頼区間
母平均の信頼度95%の信頼区間は、標本標準偏差から次の式で求めることができます。


R3~R5のデータから95%信頼区間を計算すると次のようになります。

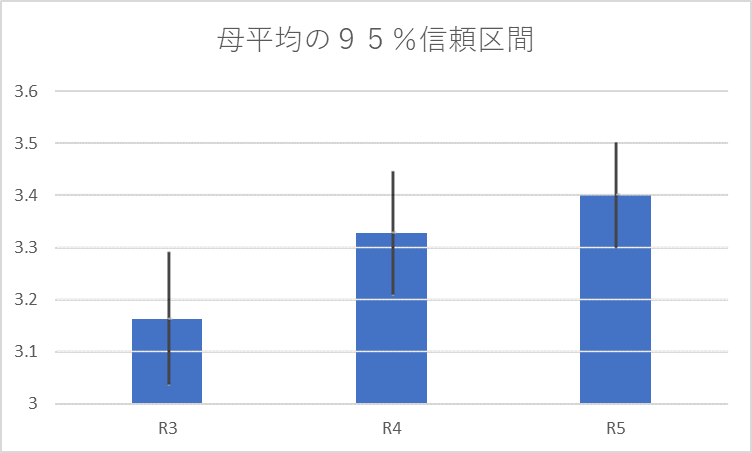
t検定と信頼区間
t検定でP<.05であれば有意差があると言えるが、信頼区間に重なりがあると有意差はないと必ず言えるかというとそうではないようです。
信頼区間に重なりがあっても片側検定で有意差があったように、信頼区間の重なり具合だけで有意差を判断せずに、正確を期するためにt検定を行いましょう。
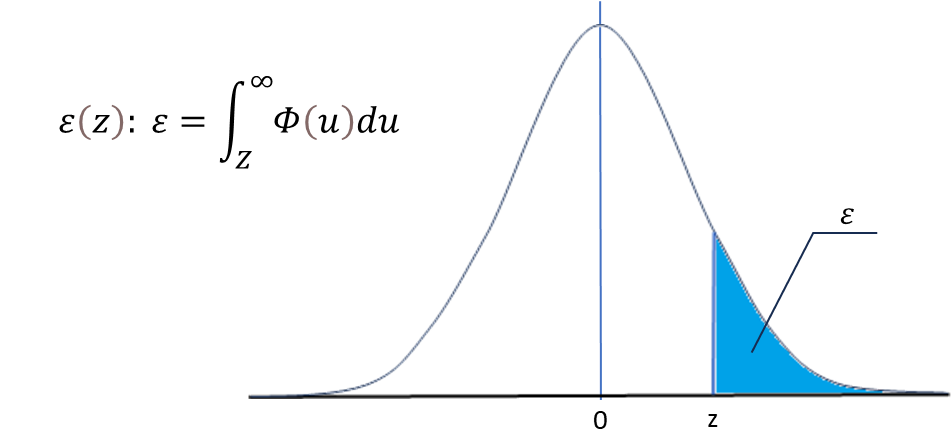
標準正規分布
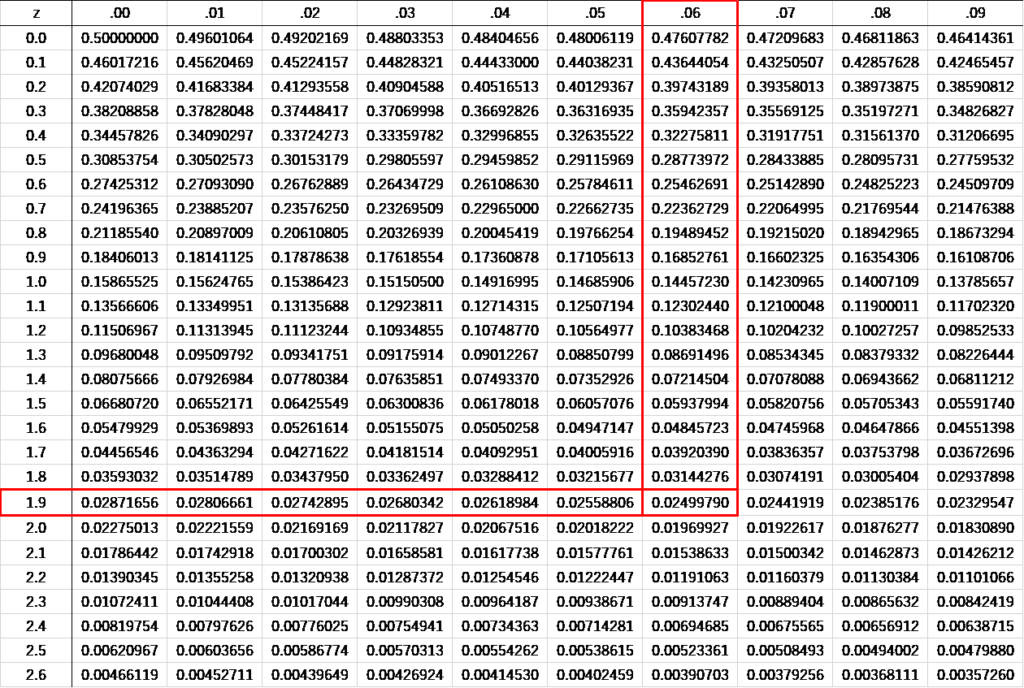
平均0、分散1の正規分布を標準正規分布と言います。下表はその分布表です。
1.96という値は有意水準5%の時の両側検定の確率面積2.5%(0.025)から求められます。
0.025に関しては関数「=NORMSINV(0.975)」を使って1.95996398という値を得ることもできます。
正規分布の上側確率