分散分析
満足度が上がっているかどうかを調べる方法として分散分析があります。「分散」とあっても分散を分析するものではなく、分散を使って母集団の平均を検定するものです。2群以上のデータに対して利用できます。
Excelのデータ分析から一元配置分散分析を選択します。
3か年の蔵書の満足度調査結果を使って検定を行います。データの個数はばらばらで問題ありません。有意水準を0.05(5%)に設定して、次のように行います。
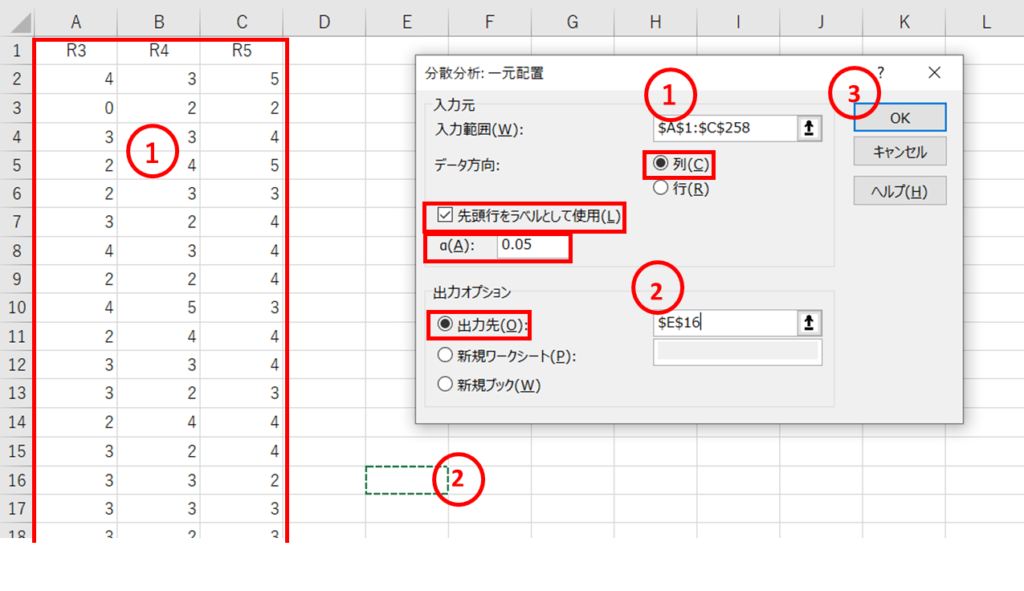
結果は以下のとおりです。

帰無仮説は、「3つのデータ群に差はない」です。
判定はP値で行うのでした。
P値は0.05以下ですので、帰無仮説は棄却され、3つのデータ群には差があることが検証されました。即ち、3つのデータ群が等しいと言える確率は1.3%程度であり、有意水準の5%以内ですので、3つのデータ群が等しいとは言えないとなります。
F値で判定する場合は、観測された分散比がF境界値より大きいことで帰無仮説は棄却されると判定します。
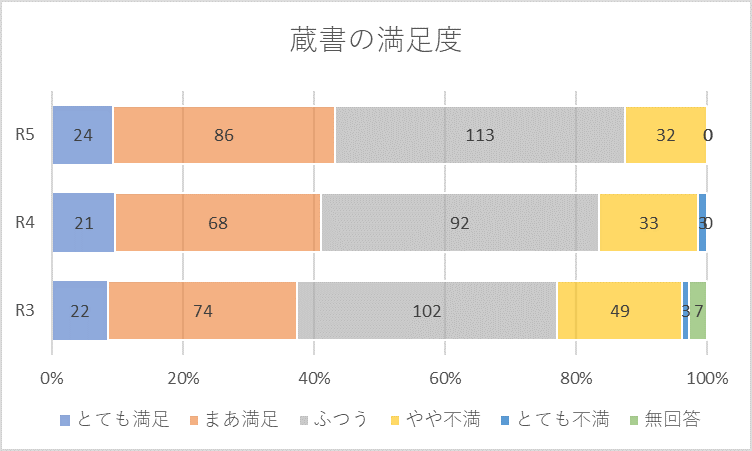
蔵書の満足度の結果を帯グラフにすると下記のようでした。見た目ではなかなか判定できないことでも、分散分析を行うことで3か年の間で蔵書の満足度の平均値が上がったことを検証することができます。
ただし、この場合の分散分析では、いずれかの年との間で有意な差があることはわかりますが、R3-R4、R4-R5、R3-R5のどの組み合わせで有意なのかまではわかりません。2群間の検定については次回行います。
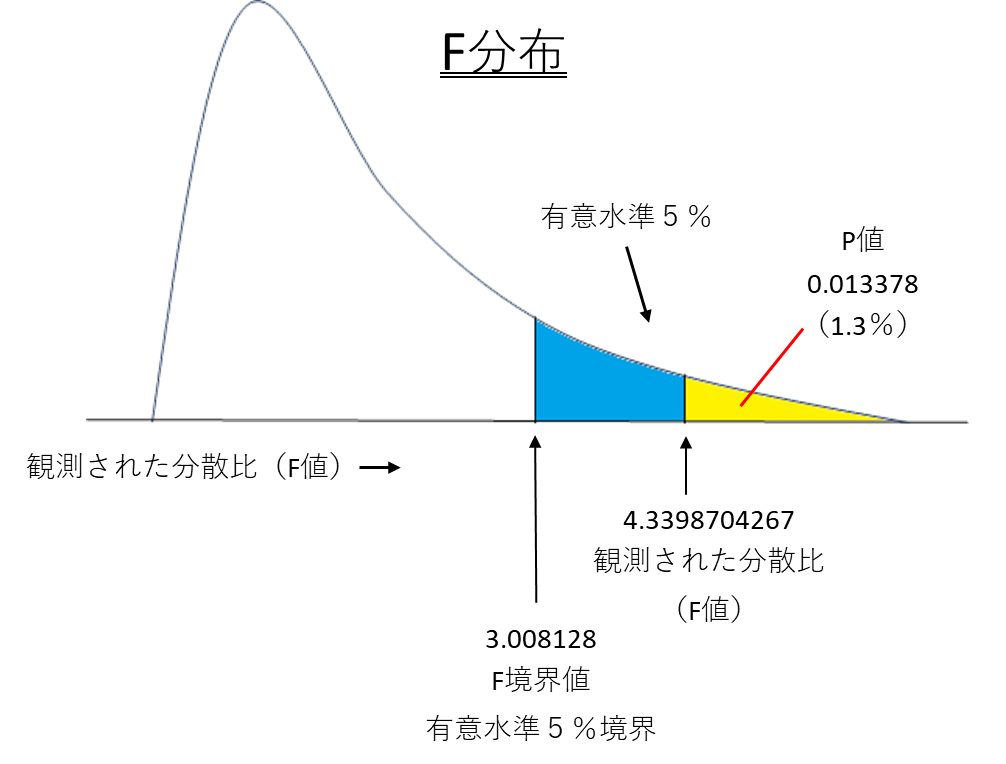
F分布
分散分析表を詳しく見てみましょう。
観測された分散比はF値と呼ばれF分布に従います。検定はこのF分布を用いて行います。
F境界値は有意水準5%の時の値です。
変動は、群間(グループ間)平方和と群内(グループ内)平方和です。平均平方和と書かれる場合もあります。ツールによって表記が異なりますが内容は同じものです。
自由度は、例えば10個のデータあった場合、9個が決まれば残りの1個は必然的に決まってしまう時、10-1=9で自由度は9になります。群の数(グループの数)やデータの個数から1を減じて算出します。
分散は、平方和(変動)を自由度で割ったものです。観測された分散比(F値)は、群間(グループ間)平方和を群内(グループ内)平方和で割ったものです。
群間平方和、群内平方和の求め方
図のような3群のデータがある場合、群間(グループ間)平方和および群内(グループ内)平方和は次のように求めます。

全データの平均を求めます。

群間(グループ間)の平方和は、各群内の平均を求め全データ平均との差を各点ごとに二乗して合算します。
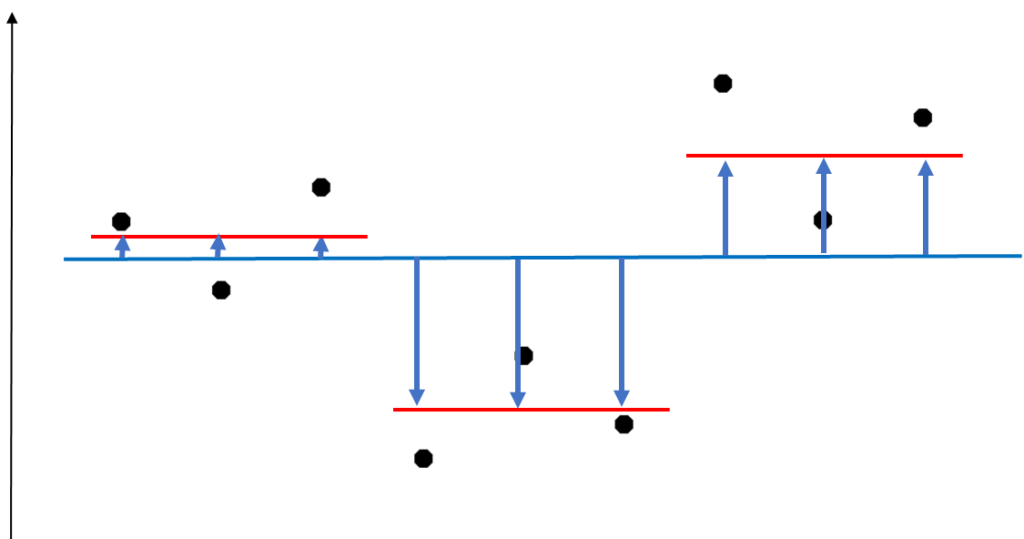

群内(グループ内)平方和は、各群内で平均値との差を求めてそれぞれ二乗して合算します。
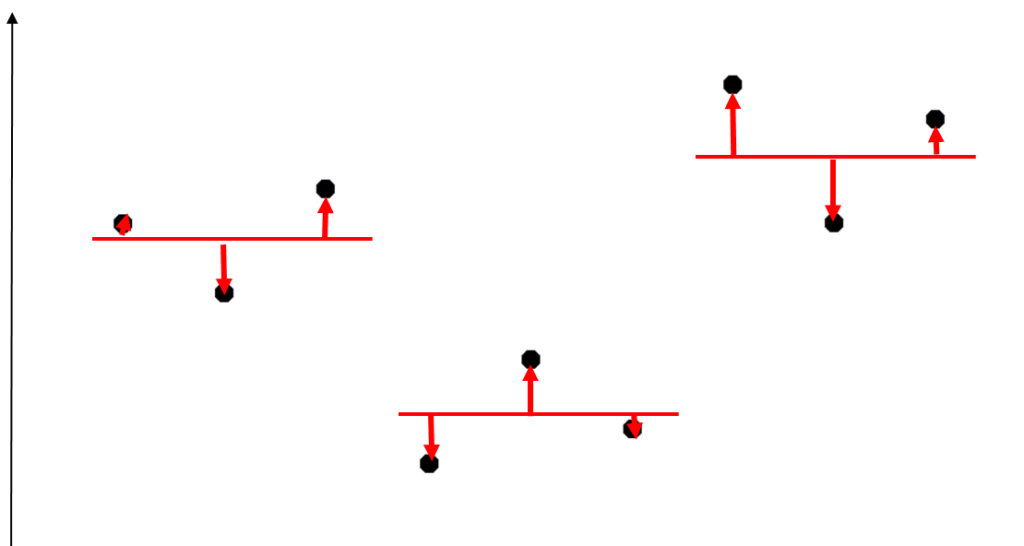
分散分析でも2群間の検定を行うことができるのですが、次回は、t検定を用いて2群間の検定を行います。