仮説検定
ここまで平均や分散、標準偏差について見てきました。これらの統計量は、満足度が去年より上がったのかどうかといったことを検証する際に使われます。統計的検証では一般に仮説検定と呼ばれる手法が用いられます。
仮説検定とは,標本を用いて母集団に統計学的に差があるかを判断する方法です。
仮説は、帰無仮説と対立仮説という二つの仮説を立てます。帰無仮説は、証明したい主張ではない方の仮説で、\(H_0\)と表します。対立仮説は、証明したい方の主張で、\(H_1\)と表します。
例えば、去年と今年のデータの間に差があることを検証したい場合、次のようになります。
帰無仮説 \(H_0\):差がない。
対立仮説 \(H_1\):差がある。
仮説検定では、「\(H_1\):差がある。」ことを証明するために、「\(H_0\):差がない。」ことを検証します。
「差」は無数に存在しその一つ一つを検証することは困難ですが、「差がない」という主張は、すなわち「等しい」という条件ひとつを検証すればよく、帰無仮説が棄却されれば対立仮説が正しいとする背理法を採ります。
P値と有意水準
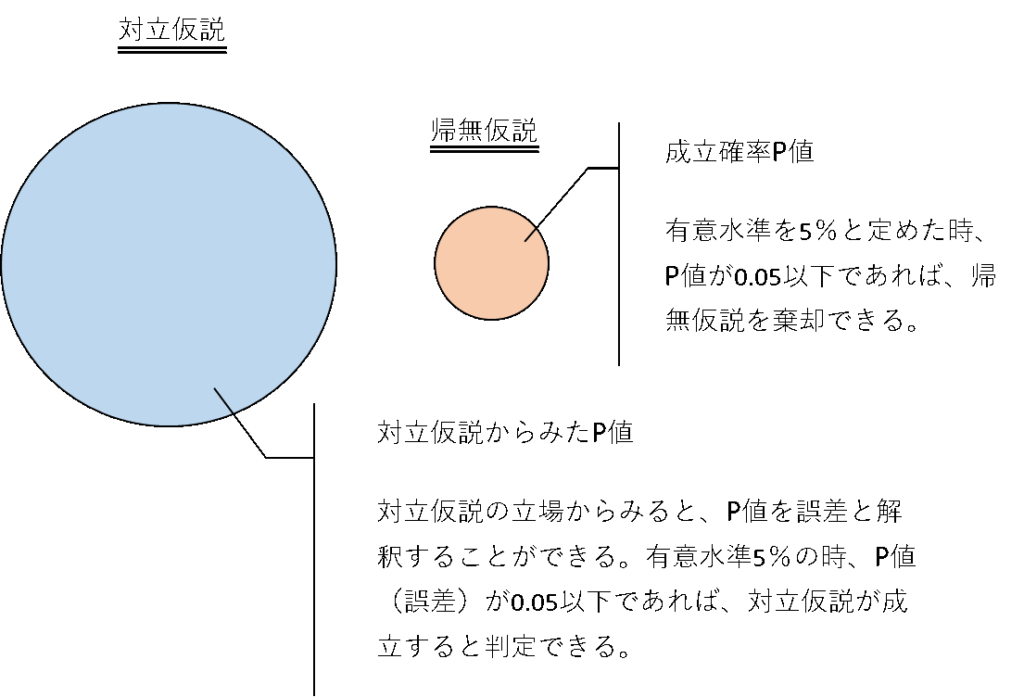
仮説検定では、「\(H_0\):差がない。」すなわち「等しい」ことが起こり得る確率(Probability)を求めて検証します。この検定で得られる確率のことをP値と呼び、このP値で仮説の採否を判定します。
例えば検定の結果、P値が0.001(0.1%)だったとすると、「等しい」ことはほとんど起こり得ないことを示しているので、「差がある」と判定されます。では、何%までであれば起こり得ないこととして判定できるでしょうか
一般には、慣用的に5%を判定の基準とすることが多いです。この値を有意水準と言います。有意水準は1%、5%、10%など、検証する対象によって予め決めておきます。P値が有意水準の値以下であれば帰無仮説は成立しないと判定されて、対立仮説が成り立つということになります。
片側検定と両側検定
対立仮説には次の3通りが考えられ、仮説検定の結果として、片側検定、両側検定という結果が示されることがあります。
ケース1 対立仮説 \(H_1\):差がある。
ケース2 対立仮説 \(H_1\):より大きい。
ケース3 対立仮説 \(H_1\):より小さい。
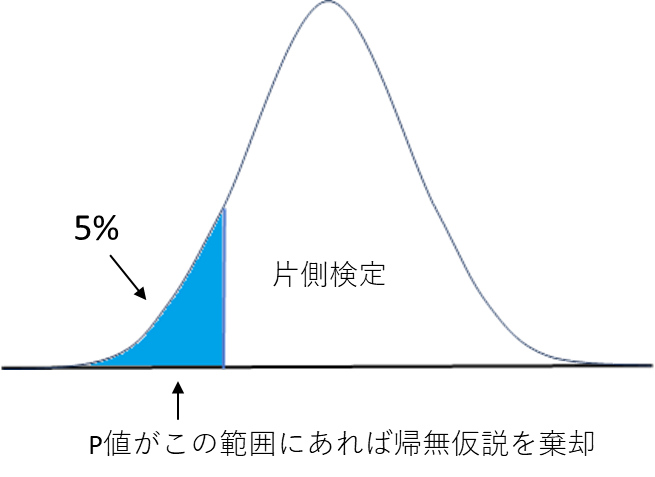
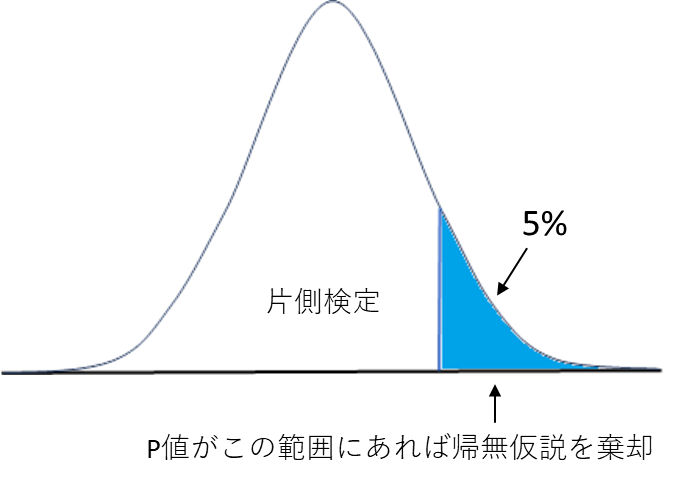
帰無仮説が起こり得る確率の分布において、有意水準が5%の時、検定は次のように行います。検定は、両側検定、片側検定の結果として提示されます。
ケース1の場合は、大きいか小さいかは関係なく差があるかどうかだけなので、分布の両側での確率が起こり得るため両側検定を行います。

ケース2,3の場合は、起こり得る確率はどちらか一方なので片側検定を行います。
統計学の基礎の残りの1%は、P値の理解でした。これで統計学の基礎は整いました。
次回からは、Excelを使った統計処理を行っていきましょう。