標準誤差
基本統計量に関する最後の説明は、標準誤差についてです。

母集団からサンプリングした標本の平均値は、母集団の真の平均値を中心に分布すると考えられます。
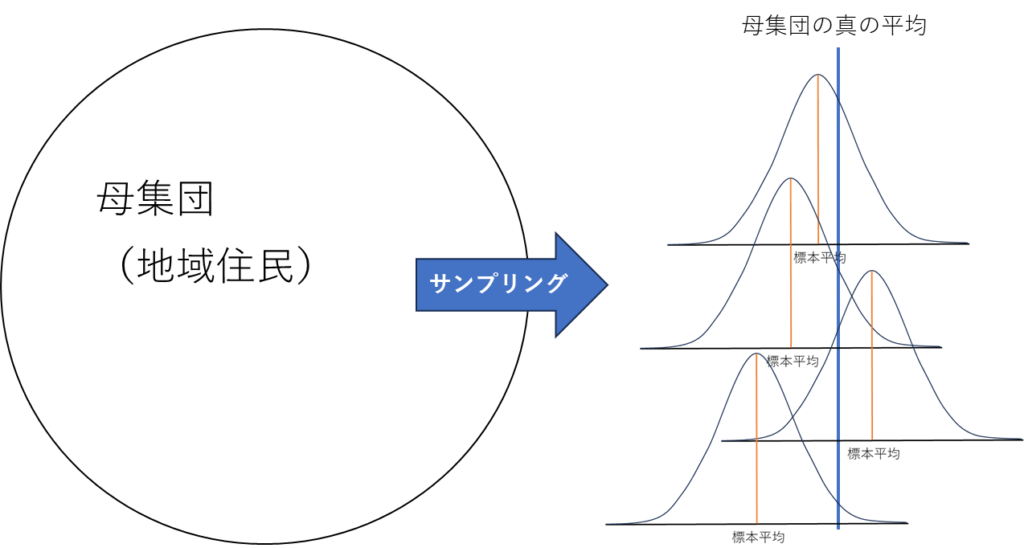
サンプリングを繰り返していくと、標本の平均値の分布は下図のように正規分布になっていきます(中心極限定理)。
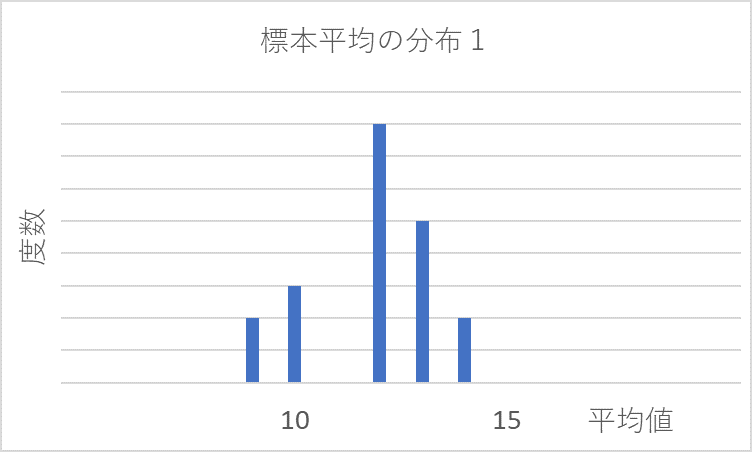
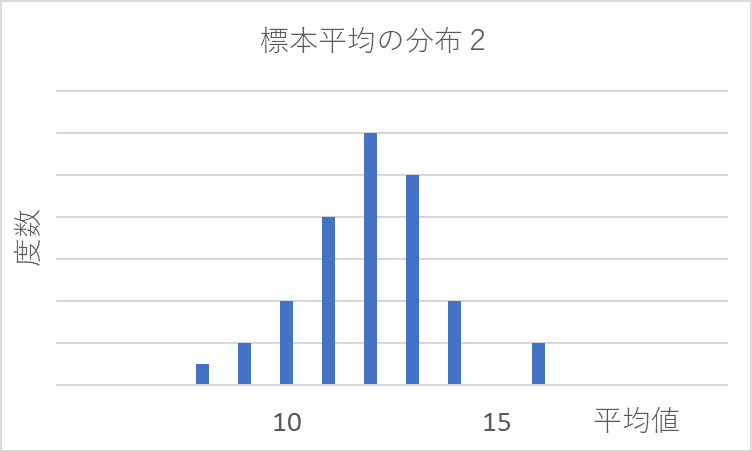
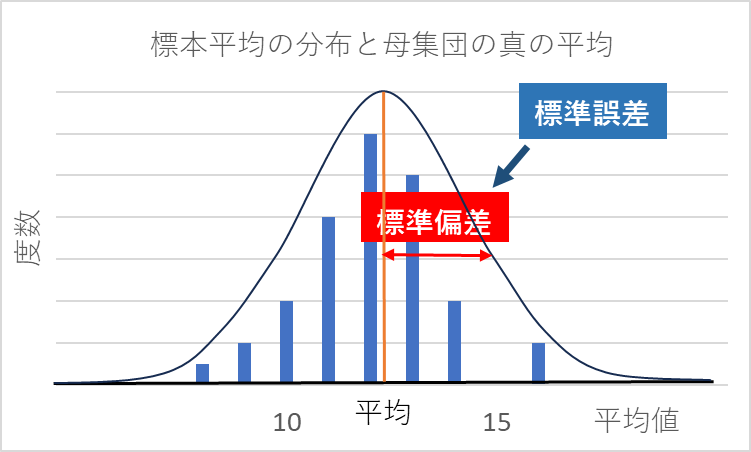
標本平均から得られる分布の標準偏差を標準誤差と言います。標準誤差はサンプリングの精度を表しており、標本平均の値が母平均に対してどの程度ばらついているかを表すものです。
誤差が少ないほどサンプリングの精度(標本の精度)が高いことを示しますが、サンプルサイズ(標本サイズ)が大きくなると標準誤差は小さくなります。
サンプルサイズ(標本サイズ)
標本の精度はサンプリングする数に関係がありますが、どの程度の数であれば母集団を推測するのに十分かつ信頼できるのかは、次の計算で求めることができます。
ここでは、賛成・反対、満足・不満足を問うような、母集団に対する比率の信頼性に注目する場合のサンプルサイズの求め方を紹介したいと思います。
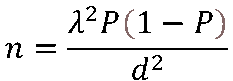
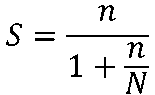
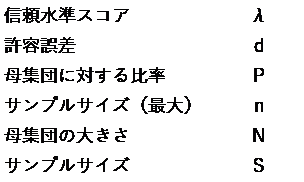
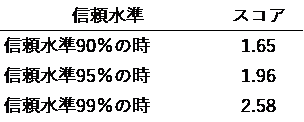
nは、母集団の大きさが未知の場合、または非常に大きい場合のサンプルサイズです。
Pは、賛成・反対、満足・不満足などの母集団での割合です。「70%が満足している」などの割合を指しますが、通常は不明なのでnの値が最大になる0.5を設定しておきます。
信頼水準スコアは、それぞれの信頼水準の標準偏差になっています。
Sは、母集団の大きさが分かっている時のサンプルサイズです。
今、信頼水準95%、許容誤差を0.05(5%)、母集団に対する比率を0.5、母集団を10,000人とした時のサンプルサイズは次のようになります。
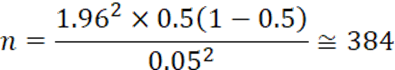
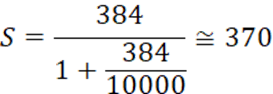
図書館利用者アンケートとサンプルサイズ
回答の精度という点でサンプルサイズを満たすことは大切ですが、図書館の利用者アンケートの場合は、統計的に有意な標本サイズがあるかどうかということよりも、少数でも利用者の意見をよく聞いてサービス向上に反映させるものなので、必ずしもサンプルサイズにこだわる必要はありません。
今後も統計的に有意かどうかということよりも、その結果を図書館のサービス向上のためにどう判断し利用するかが重要になる場面が多く出てくるでしょう。