今回は、平均、分散、標準偏差について見ていきます。これらの文字を見ると、本を閉じてしまう人もいるかもしれません。
しかし、よく読んでみると、分散、偏差など内容は何も難しいことは言っていないのです。馴染みのない用語には難しいイメージを抱いてしまい勝ちですが、まずは一歩を踏み出してみましょう。
平均と偏差
Excel「データ分析」の基本統計量では下図の赤枠の箇所に記載されています。
今回は少し数式を使います。
今、データの数を\(n\)個とし、変数(データ)を\(x_1\)、\(x_2\)・・・\(x_n\)とします。
この時、平均\(\bar{x}\) は次のようになります。
\(\bar{x}\) =\(\frac{1}{n}\)(\(x_1\)+\(x_2\)+・・・+\(x_n\)) (\(i\) = 1、2、3・・・・n)
そして、変数と平均との差(\(x_i\)-\(\bar{x}\))のことを偏差と言います。
馴染みのない偏差という用語がでてきますが、単に平均との差分のことを言っているだけで難しい内容ではありません。
そして、この平均と偏差の二つの統計量こそが統計学の土台となっているものなのです。
分散と標準偏差
偏差は、(\(x_1\)-\(\bar{x}\))+(\(x_2\)-\(\bar{x}\))+・・・+(\(x_n\)-\(\bar{x}\))のようにすべてを足し合わせるとゼロになってしまうため、この偏差を有効活用するために\((\)\(x_i\)-\(\bar{x}\)\()^{2}\)と二乗(平方)してすべて正の値にして用います。
\(Z\)=\((\)\(x_1\)-\(\bar{x}\)\()^{2}\)+\((\)\(x_2\)-\(\bar{x}\)\()^{2}\)+・・・+\((\)\(x_n\)-\(\bar{x}\)\()^{2}\)=\(\sum_{i=1}^{n}\)\((\)\(x_i\)-\(\bar{x}\)\()^{2}\)
この\(Z\)のことを偏差平方和(単に平方和とも)と言います。偏差を二乗したものを足し合わせたものです。
ここから分散と標準偏差が次の式で与えられます。
分散 \(V\)=\(\frac{Z}{n}\)
標準偏差 \(s\)=\(\sqrt{V}\)
分散も標準偏差もデータのばらつき具合、広がり具合を表わしています。分散は二乗の値になっているので標準偏差ではその平方根をとっています。
偏差は平均との差ですから、分散も標準偏差も値が大きいほどばらつきが大きいことを示します。
下図のように平均と標準偏差でばらつきを表現できる左右対称の分布を正規分布と言います。標準偏差は平均から変曲点までの距離を示しています。
基本統計量では、分散や標準偏差の値を見ることで、データの分布形状を把握することができます。上記の基本統計量の表では、R3からR5へ次第にばらつきが小さくなっている様子を見ることができます。
ここまで、平均と偏差およびその変形しか説明していませんが、ここまでが分かれば統計学の基礎の90%は理解できたといって良い内容です。
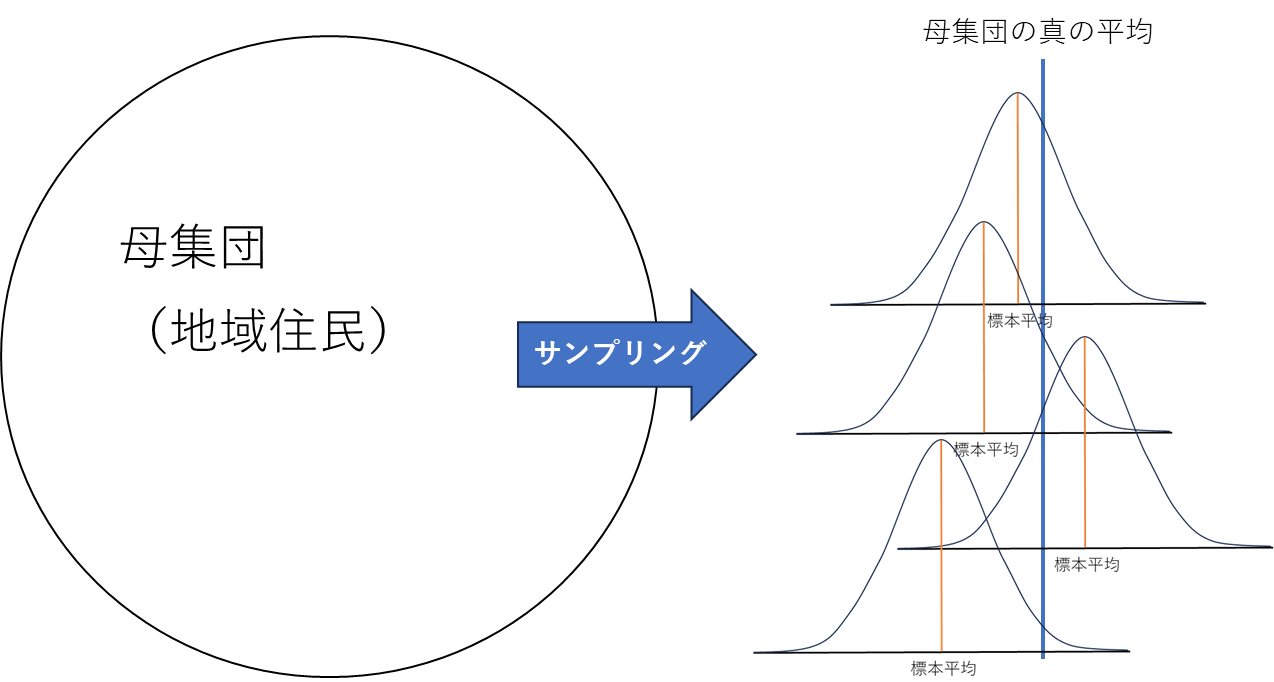
記述統計と推測統計
ある集団からデータ\(n\)個をサンプリング(抽出)した場合、ある集団を母集団と言い、サンプリングしたデータを標本と言います。
ここで、分散の導出の際に、偏差平方和\(Z\)を\(n\)-1で除す場合を不偏分散と言い、標本数\(n\)に基づいて母集団を推測するときに用います。
実は、Excelの基本統計量は実際の満足度などの標本データをもとに、不偏分散を用いて母集団の平均、分散、標準偏差を推測した値になっています。
そのため、基本統計量と同じ結果を得るためには分散の導出に\(V\)=\(\frac{Z}{n-1}\)を使って計算する必要があります。
すなわち、統計学には標本そのものを対象にした記述統計と標本から母集団を推測する推測統計があることを知る必要があるのです。(※)
標本そのものの統計量を知りたい場合と、標本から母集団を推測する場合との違いについてまとめると次のようになります。

標本ではサンプル数\(n\)が分かっているので、標本の分散を知りたい時は\(n\)を使います。標本から母集団を推測する場合は\(n\)-1を用いて分散を計算します。
\(\frac{1}{n-1}\)\(>\)\(\frac{1}{n}\)なので、母集団の分散は標本の分散より大きくなる(ばらつきは標本より大きいと考えられる)と覚えておくと良いでしょう。
ここまでが理解できれば、統計学の基礎の99%に到達したと考えて良いでしょう。
母集団と標本
図書館における母集団とは、図書館サービスを提供する対象である市民、地域住民ということになるでしょう。
母集団を図書館利用者とする考え方もあるかも知れません。この場合、特定の集団を準母集団と言うこともあります。
母集団を地域住民だとすると、アンケートは母集団からのサンプリングに相当し、アンケートの結果が標本データということになります。
母集団の全員を調査することは困難なので、サンプリングして標本をとることで母集団を推測しようとするわけです。

ところで図書館の現場では、このアンケート結果は母集団を推測する標本データであると捉えているでしょうか。
図書館利用者に限定したアンケート結果であって、地域住民全体が推測できる情報だとは思っていないかも知れません。
そしてそのことが、去年より増えた、減ったという記述統計の範囲での分析に留まっている理由にほかならない気がするのです。
これから扱う統計はすべて推測統計です。不偏分散が使われます。
たとえ公表するアンケート結果報告が記述統計に基づくものであったとしても、内々には図書館サービスの対象である母集団に関する分析でなければ、地域住民の図書館利用増加やサービス向上にはつながらないでしょう。
推測統計の視点を持つことで、アンケートの質問の仕方や地域住民の見方が新たに変わることでしょう。
\(n\)-1の話
なぜ、\(n\)-1なのか。この説明はなかなかむずかしいようですが、次のような説明があります。
標本は母集団の一部であり、母集団全体は標本より広がりを持った値を含んでいると考えられます。すなわち、母集団の分散は、標本の分散よりは大きいということです。
母集団の分散 ≧ 標本の分散
この差は、母集団の分散との誤差と考えられるので、以下の式を考えます。
母集団の分散 = 標本の分散 + 誤差
ここで、母集団の分散を\(\sigma^{2}\)、標本の分散を\(V\)、サンプリングのたびに\(\bar{x}\)は変化するので誤差を標本平均の分散\(\frac{\sigma^{2}}{n}\)とし、以下の等号がほぼ成り立つものとして説明しています。
\(\sigma^{2}\)=\(V\)+\(\frac{\sigma^{2}}{n}\)
=\(\frac{Z}{n}\)+\(\frac{\sigma^{2}}{n}\)
\(\sigma^{2}\)-\(\frac{\sigma^{2}}{n}\)=\(\frac{Z}{n}\)
\(\sigma^{2}\)\((\)\(\frac{n-1}{n}\)\()\)=\(\frac{Z}{n}\)
\(\sigma^{2}\)=\(\frac{n}{n-1}\)・\(\frac{Z}{n}\)
\(\sigma^{2}\)=\(\frac{Z}{n-1}\)
※他には、ベイズ統計や多変量解析などがあります。