図書館の利用者数がどのような分布になるのかを予め知ることができれば、それは何かと見積もる上で有益な情報となります。
入館者数、カウンターでの貸出者数、自動貸出機利用者数などのそれぞれの状況を予測することで職員体制はより確かなものになるでしょう。ここでは、想定する平均値から利用者数の分布を推測することを考えていきます。
図書館はガンマ分布!
図書館の1時間ごとの来館者数や貸出者数などの分布は、平均値を中心に左右対称になる正規分布ではなく、最頻値をピークに右側(値が大きい方)へなだらかに裾野広がる形になっています。
こういった分布は、人の体重や製品部品の寿命、ウイルスの潜伏期間などで見られ、下記のガンマ分布に従う現象として知られています。
$$f(x)=\frac{λ^{k}}{Γ(k)}x^{k-1}e^{-λx}$$
ガンマ分布は、「期間1/λあたりに1回起こると期待されるランダムな事象がX回起こるまでの時間の分布」という意味になります。式は難しそうな形をしていますが、Excelのガンマ確率密度関数(GAMMA.DIST関数)を用いると容易に計算することができます。
GAMMA.DIST(X、α、β、関数形式)
X :回数(ここでは人数
α :形状パラメータ
β :尺度パラメータ
形式 :FALSE=確率密度、TRUE=累積確率密度
来館者数の1時間平均を19人として、早速この場合のガンマ分布を見てみましょう。各パラメータは以下のように計算します(注:値は、有効桁数の多いExcelでの計算結果)。
1時間平均 =19人/時
1分平均(λ) =0.3167人/分 1分当たりの来館者数。60で割る。
形状パラメータα =6.0167 平均値とλの積
尺度パラメータβ =3.1579 λ分の1(1/λ)
対象時間 =7時間(例) 10時から17時を対象。
Excelでは、平均と対象時間を設定すると他の値は自動計算するようにしておきます。ガンマ確率密度関数の計算では各値のセルを参照するようにします。下記の表の確率と累積確率(A)の列でGAMMA.DIST関数を使います。
確率の列では関数形式をFALSE、累積確率(A)の列では関数形式をTRUEにします。
人数がX人以上になる確率を調べるために累積残(B)=1-(A)を求め、その逆数1/(B)で発生頻度(時間換算)を算出します。さらに発生頻度(時間換算)を対象時間で除すことで日数換算での発生頻度を求めます。

計算結果の確率密度分布を図示すると以下のようになります。
最頻値は確率の列で値が最も大きい箇所の人数が該当し、16人となっています。15人もほぼ同じ値の確率であり、このあたりが最頻値と予測されます。
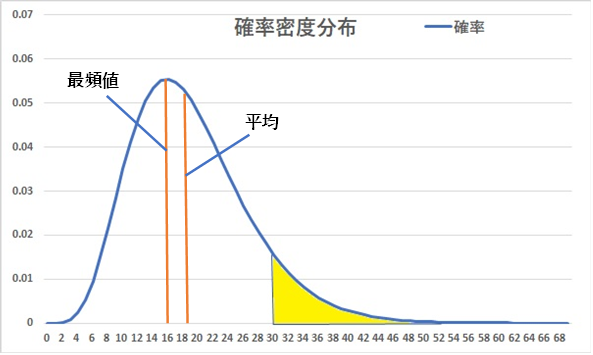
【ガンマ分布計算結果の見方】
[例1]1時間に30人以上が来館する発生頻度(日数換算)は、約1.6日となっています。これは、1.6日の間のどこかの1時間で発生する、ということを示しています。確率分布の図では黄色の部分(30人以上の発生確率)を計算していることになります。
[例2]1時間に40人以上が来館する発生頻度(日数換算)は、約10日となっています。これは、10日に1回、月に3回くらいは1時間40人以上来館することがあることを示しています。
[例3] 1時間に56人以上が来館する発生頻度(日数換算)は、約355日となっています。約1年に1回発生する頻度です。これ以上の頻度は稀なケースであると判断できます。
実際の様子は?
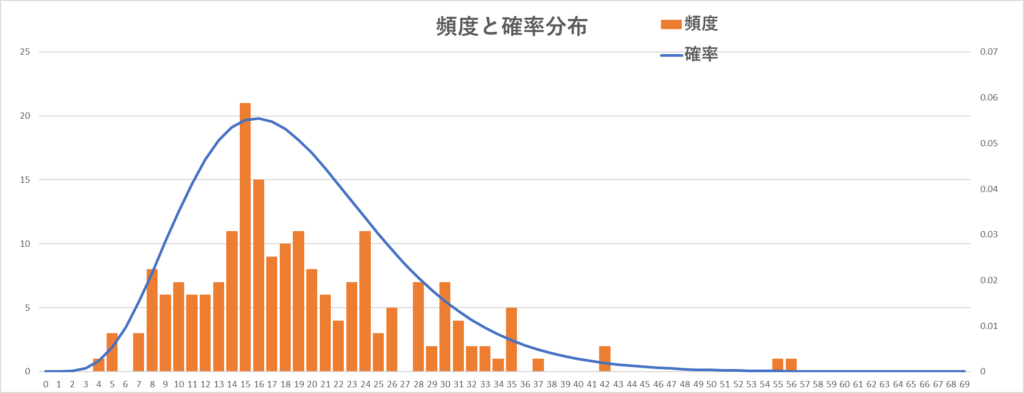
平均が19人となるデータでは、基本統計量(※)は下表のとおりでした。ガンマ分布と実際の頻度数の棒グラフとを重ね合わせた図を下記に示します。
実際のデータはガンマ分布の曲線に沿ってはいませんが、3人単位のヒストグラム(※)との重ね合わせでは、ほぼ分布に従っている様子が見て取れます。
ガンマ分布で考察する目的は、平均値から利用者数の分布を推測することでした。この例では、通常1時間の来館者が15~16人(最頻値)のところ、その倍の30人以上が来館する頻度はおよそ1日半ごとに発生し、40人以上が来館する可能性が月に3回くらいはあることが予め分かるのでした。
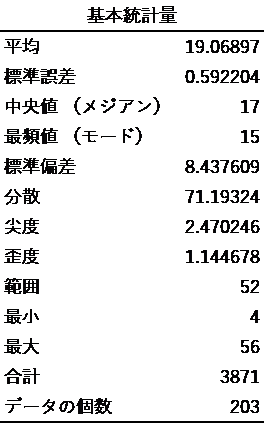
※基本統計量、ヒストグラムは、Excelタブのデータ⇒データ分析で算出・作成できます。データ分析が表示されていない場合は、ファイル⇒オプション⇒アドインで設定します。
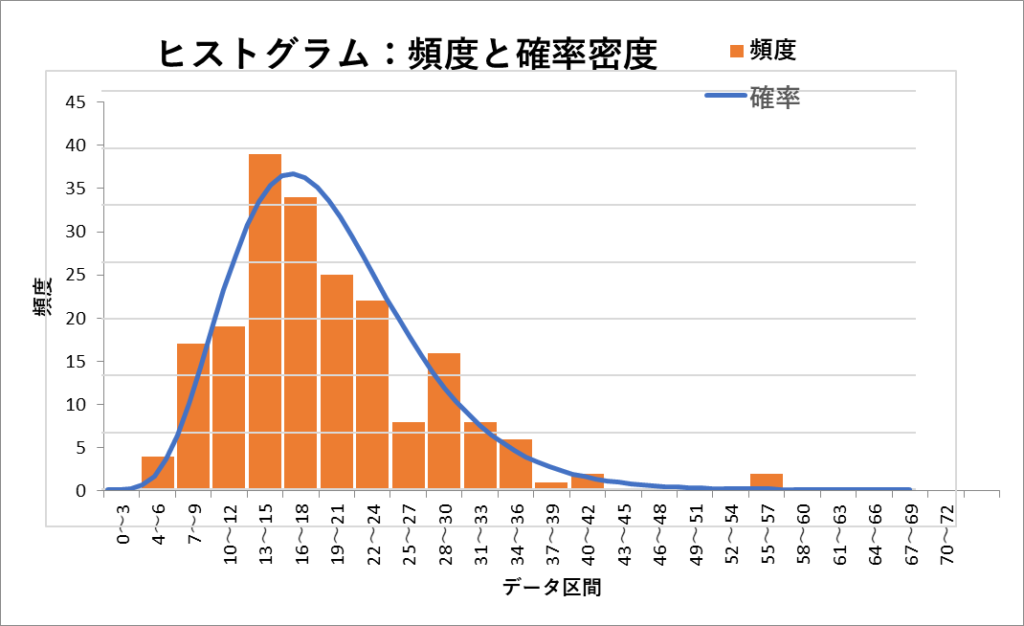
最頻値と平均値で注意すべきこと
最頻値と平均値に関して注意すべき点について述べておきたいと思います。
平均はいくらかと問われて、最小値から最大値までのばらつきを勘案して平均を答えることは、実はかなり困難なことで、「普段はだいたいこれくらいの人数」と答えるのは最頻値のことを指していると考えられます。
正規分布では平均と最頻値が同じで左右対称の分布になりますが、図書館ではガンマ分布の場合が多いので、最頻値から逆算して平均値を導き出すことも必要になってきます。平均がどれくらいかを聞くよりも、どのくらいの人数の時が多い?と聞く方が正確に把握できる場合もありそうです。
最頻値から平均値を求める
以下はガンマ分布の場合で、最頻値から平均値を求める方法の説明です。
形状母数を\(k\)、尺度母数を\(θ\)とし、\(θ=\frac{1}{λ}\)とすると、平均は \(kθ=\frac{k}{λ}\)、最頻値は \((k-1)θ=\frac{k-1}{λ}\)で表わされます。
ここで\(θ=60\)(分)とし、求める平均を\(x\)とすると、\(λ=\frac{x}{60}\)です(平均を60で除す)。
そこで最頻値は、\(x\)を使って次のように書き表わすことができます。
$$(k-1)θ=\frac{k-1}{λ}=\frac{k}{λ}-\frac{1}{λ}=x-\frac{60}{x}$$
今、最頻値が15であれば \(15=x-\frac{60}{x}\)となり、これを計算すると、
\(x-15=\frac{60}{x}\)
\(x(x-15)=60\)
\(x^{2}-15x-60=0\)
二次方程式の解の公式を使って \(x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\)
$$x=\frac{15\pm\sqrt{15^{2}+4\times60}}{2}=18.28 ( 正の値のみ計算) $$
最頻値が16であれば、
$$x=\frac{16\pm\sqrt{16^{2}+4\times60}}{2}=19.14 ( 正の値のみ計算) $$
それぞれ最頻値に対応する平均値を求めることができました。
1時間を母数としたガンマ分布の場合、最頻値から平均値を求める式を一般化すると次のとおりとなります(注:正の値のみ計算)。
$$平均値=\frac{最頻値+\sqrt{最頻値^{2}+4\times60}}{2}$$
平均がわかっていればその値を使い、最頻値の場合は逆算して平均値を求め、ガンマ分布で利用者数の推測を行うことができます。
それぞれの図書館の実際に適用してみると、これまでの理解とは異なる新たな知見が得られるかも知れません。